УДК 532.5: 622.276

https://doi.org/10.26516/2541-9641.2025.3.225

EDN: SHJIME

Разработка однородного пласта на основе модели плоскорадиальной двухфазной фильтрации несмешивающихся жидкостей для газоводонапорного режима

Н.Э. Курдагия, В.Д. Ворошилова

Армавирский механико-технологический институт (филиал) ФГБОУ ВО КубГТУ, г. Армавир, Россия

Аннотация. Представлено решение задачи двухфазной фильтрации несмешивающихся жидкостей в однородном пласте при газоводонапорном режиме эксплуатации скважин.

Ключевые слова: задача разработка, однородный пласт, модель, двухфазная фильтрация, несмешивающиеся жидкости, водонапорный режим

При проектировании и разработке месторождений нефти и газа в пористой среде важно изучать течение нескольких флюидов одновременно. Как правило, это газ, нефть и вода, являющиеся отдельными фазами, не смешивающимися друг с другом.

Месторождение образуется в результате вытеснения первоначально залежавшейся здесь воды из продуктивных пластов (Желтов, 1998). Поэтому вместе с нефтью и газом в пластах содержится определенное количество пластовой воды.

Рассмотрим простейшее двухфазное течение жидкости, соответствующее вытеснению жидкости, первоначально заполнившей поры, другой жидкостью, не смешивающейся с первой жидкостью. В основном нефть вытесняется из пласта водой (реже газом). Этот процесс является основным как в случае естественного водонапорного режима (например, при внедрении в пласт пластовой воды или газовой шапки, выталкивающей нефть к добывающим скважинам), так и при вторичных способах добычи нефти. добыча (например, закачка жидкости или газа через систему нагнетательных скважин с целью поддержания пластового давления и перемещения нефти в добывающие скважины).

Если пренебречь капиллярными силами и влиянием силы тяжести, а также при малом поверхностном натяжении между фазами, то процесс смещения можно представить простым математическим описанием. Впервые такое описание было предложено американскими исследователями С. Бакли и М. Левереттом в 1942 году. Математическое описание основано на таких понятиях, как насыщенность, относительные фазовые проницаемости и закон Дарси. Такой анализ одномерных потоков позволяет выявить основные эффекты и характерные особенности совместной фильтрации двух жидкостей.

Давайте рассмотрим процесс репрессий. На рисунке изображен образец однородной и изотропной пористой среды, направление потока горизонтальное. Пусть ω — площадь поперечного сечения образца и предположим, что она достаточно мала, чтобы давление и насыщение можно было считать постоянными по поперечному сечению. Ввиду пренебрежения капиллярным давлением давление в нефтяной и водной фазах предполагается одинаковым, фазы несжимаемыми, а температура постоянной.

Образец, представленный на рисунке изначально заполнен маслом. Далее через секцию х = 0 прокачивается вода. В период вытеснения нефти водой образуется зона совместного движения жидкостей. В процессе совместного течения фаз в пористой среде хотя бы одна из них образует связную систему, которая будет граничить со скелетом породы и частично со второй жидкостью.

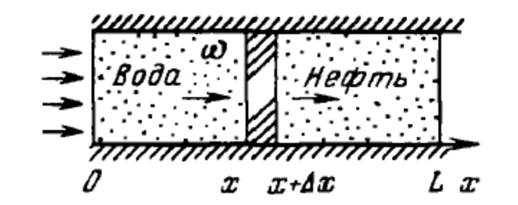
Рисунок. Схема вытеснения нефти водой.

Figure.The scheme of oil displacement by water

Площадь взаимодействия каждой фазы со скелетом пористой среды значительно превышает площадь контакта между фазами. Это говорит о том, что основной вклад в сопротивление движению вносит взаимодействие каждого компонента жидкости с твердым скелетом пласта, и эффектом увлечения одной жидкости другой в первом приближении можно пренебречь. При этом сопротивление, которое испытывает каждая из фаз при совместной фильтрации, отличается от сопротивления, которое существовало бы, если бы текла только одна из них. Экспериментально установлено, что скорость потока каждой фазы увеличивается с увеличением насыщенности и градиента давления.

Закон фильтрации для каждой фазы можно представить в дифференциальной форме в виде закона Дарси (Сборник задач…, 1985; Олховская, 2006):

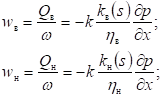 (1)

где wв, wн скорости фильтрации воды и нефти; Qв, Qн – объемные расходы воды и нефти; 𝜂в, 𝜂н – коэффициенты динамической вязкости фаз; kв(s), kн(s) – относительные фазовые проницаемости; s = sв – водонасыщенность. Водо- и нефтенасыщенность связаны соотношением:

s_в + s_н = 1. (2)

Сформулируем закон сохранения массы каждой фазы. Для воды изменение массы находится согласно направления течения по оси x, плотность ρ_в будет постоянной исходя из предположения о несжимаемости. Через сечение x (рис.) за время ∆t втекает в объем ∆V масса воды ρ_в ω×w_в (x, t)×∆t, а вытекает через x + ∆x масса ρ_в∙ω∙w_в (x + ∆x, t)∙∆t.

Таким образом, изменение массы воды в ∆V за время ∆t будет равняться:

, (3)

где

. (4)

Необходимо, чтобы изменение массы было сбалансировано за счет изменения во времени водонасыщенности в поровом объеме:

. (5)

Приравняв два последних выражения, и поделив обе части равенства на ρв∙∆V×∆t и перейдя к пределу при ∆x → 0, ∆t → 0, получаем:

или . (6)

Таким же способом выводится уравнение сохранения массы нефти:

. (7)

Учитывая (2) формулу (7) можно представить:

. (8)

Просуммировав уравнения неразрывности (6) и (8) для обеих фаз, получаем:

. (9)

Отсюда находится первый интеграл:

 или . (10)

Уравнения (9) и (10) показывают, что суммарная скорость двухфазного потока w(t), как и суммарный расход фаз Q(t), не зависят от x, т.е. постоянное значение или известная функция. Это является следствием предположения о несжимаемости фаз.

Уравнения (1), (6), (8) или (10) полностью описывают процесс перемещения и позволяют определить неизвестные функции s(x,t), w_в(x,t), w_н(x,t) и p(x,t). Проведя небольшие расчеты, можно получить уравнения, содержащие только водонасыщенность.

Из (1) исключим градиент давления, разделив одно уравнение на член другого. Мы получаем

:, (11)

где

Применяя правило производных пропорций и с учетом формулы (10),

получаем:

 (12)

Введем обозначение:

 (13)

Из выражения (12) находим:

 и  (14)

Функцию насыщения f(s) называют функцией распределения фазового потока или функцией Бакли – Леверетта (Нигматуллин, 1987). Формула (14) показывает, что соотношение скоростей фильтрации вытесняющей фазы и суммарной скорости равно объемной доле воды в суммарном потоке двух фаз. Функция f(s) играет существенную роль в гидродинамических расчетах двухфазных потоков; оно определяет полноту вытеснения, а также характер распределения насыщенности по пласту.

Задача повышения нефтеотдачи сводится к применению на пласт таких воздействий, которые имеют вид f(s) в сторону увеличения полноты вытеснения.

Из формулы (13) следует, что f(s) полностью определяется относительными фазовыми проницаемостями. Подставив (14) для wв в уравнение (6), получим:

 (15)

Поскольку насыщенность зависит от двух переменных s = s(x,t ), то

используя дифференцирование сложной функции к , получим:

 (16)

Сделав некоторые преобразования, приводим (1.29) к виду:

 (17)

Формула (17) является дифференциальным уравнением только отно-сильно насыщенности. Решив уравнение (17), независимо от распределения давления p(x,t), можно получить изменение насыщенности во времени по пласту. Данное обращение носит название Бакли – Леверетта, в честь авторов.

Для нахождения распределения насыщенности к (17) необходимо добавить начальное и граничное условия. Они могут задаваться как некоторые функции, либо константами. Случай кусочно-постоянных начальных данных имеет важное (Брусиловский, 2002) значение в практике. Значение исходной водонасыщенности влияет на технологические процессы и определяет структуру зоны вытеснения.

Литература

Желтов Ю.П. Разработка нефтяных месторождений: Учеб. для вузов. Москва : ОАО «Издательство «Недра», 1998.

Сборник задач по разработке нефтяных месторождений : учеб. пособие для вузов / Ю.П. Желтов, И.Н. Стрижов, А.Б. Золотухин, В.М. Зайцев. Москва : Недра, 1985.

Ольховская В.А. Расчет показателей разработки однородного пласта на основе модели двухфазной фильтрации для жесткого водонапор-ного режима (плоскорадиальное движение). Методические указания. Самарский государственный технический университет, 2006.

Нигматуллин Р.И. Динамика многофазных сред. В 2 ч. Ч. 1. Москва : Наука, 1987. 464 с.

Брусиловский А.И. Фазовые превращения при разработке месторождений нефти и газа. Москва : Грааль, 2002. 579 с.

Курдагия Нугзар Эльдарович,

ассистент кафедры машин и оборудования, нефтяных и газовых промыслов,

Армавирский механико-технологический институт (филиал) ФГБОУ ВО КубГТУ,

352905, Краснодарский край, г. Армавир, ул. Кирова, д. 127,

тел.: 8(918)676-62-48,

электронная почта: k@nugzar-e.ru.

Ворошилова Виктория Дмитриевна,

студент кафедры машин и оборудования нефтяных и газовых промыслов,

Армавирский механико-технологический институт (филиал) ФГБОУ ВО КубГТУ,

352905, Краснодарский край, г. Армавир, ул. Кирова, д. 127,