УДК 551.24

https://doi.org/10.26516/2541-9641.2025.4.193

EDN: OVMGYU

Физическое моделирования сейсмогенной активизации разлома *

С.А. Борняков¹, И.А. Пантелеев², А.Н. Шагун¹, А.А. Каримова^1,3, Д.В. Салко¹

¹Институт земной коры СО РАН, г. Иркутск, Россия

²Институт механики сплошных сред УРО РАН, г. Пермь, Россия

³Иркутский государственный университет, г. Иркутск, Россия

Аннотация. Выполнено физическое моделирование сейсмогенной активизации разлома по механизму “stick-slip” в упруго-пластичной модели литосферы с комплексной инструментальной регистрацией деформационного процесса в модели. Компьютерная обработка полученных с моделей фотографий методом корреляции цифровых изображений и результаты обработки данных с лазерных датчиков и акселерометров позволили установить что:

— деформации в крыльях модельного разлома реализуются в низкочастотном колебательном режиме, при постоянной скорости нагружения модели, с отличающимися частотами и амплитудами колебаний в активном и пассивном крыльях;

— рост напряжений в модели сопровождается уменьшением частоты колебаний и увеличением их амплитуды;

— импульсная активизация модельного разлома предваряется автоволновым деформационным процессом в высокочастотной области (4–14 Гц) с последующим уменьшением преобладающих частот в 2 раза и ростом амплитуды в 1.5 раза.

Ключевые слова: физическое моделирование, разлом, деформация, очаг землетрясения, сейсмогенная активизация, спектр колебаний.

Введение

Сильные тектонические землетрясения в пределах урбанизированных территорий приводят к многочисленным человеческим жертвам и разрушениям социальной и промышленной инфраструктуры. Продолжительные исследования широкого круга специалистов разного профиля, направленные на создание способа превентивного краткосрочного прогноза сейсмических катастроф, пока не дали желаемого результата. Тем не менее, поиски путей решения этой прогнозной проблемы продолжаются и с учетом активного развития геофизических и компьютерных технологий возможность её решения, не так давно ставившаяся под сомнение (Geller et al., 1997) уже не кажется недостижимой.

В основе прогноза любого малоизученного природного процесса, в том числе и землетрясения, должна лежать его теоретическая модель, адекватно объясняющая разные явления, наблюдавшиеся перед ним и классифицируемые как их предвестники (Cicerone et. all., 2009). Существуют более десяти моделей землетрясений, из которых наиболее востребованной является модель прерывистого скольжения “stick-slip”, согласно которой сейсмические события обязаны своим происхождение периодической сейсмогенной активизации разломов, составляющих внутреннюю структуру крупных сейсмических зон (Brace, Byerlee, 1965). Известны многочисленные примеры экспериментального воспроизведения этой модели в лабораторных условиях. В более ранних экспериментах в основном использовались модели из горных пород или близких к ним по механическим свойствам искусственных материалов. Позже, по мере развития производства полимерных материалов, реологический спектр используемых моделей существенно расширился. Результаты этих многочисленных экспериментов, ставивших акцент на инструментальную регистрацию физических процессов, предшествующих импульсной активизации модельного разлома, позволили лучше понять процесс подготовки землетрясения в природе и расширить перечень предвестников, проявляющихся в предсейсмогенном его состоянии.

Из всего многообразия полученных экспериментальных работ отметим одну (Ma et al., 2012), в которой дано синергетическая трактовка деформационной эволюции межблокового контакта в критическом состоянии, созвучная с ранее предложенной П. Баком и К. Тангом моделью очага землетрясения как самоорганизованной критичности (Bak, Tang, 1989) и способствующая переходу прогнозных исследований на качественно новый уровень. Представленные в цитируемой работе результаты показали, что при придельном уровне накопленных напряжений на контакте двух блоков процесс их импульсного смещения относительно друг друга предваряется двумя стадиями деформации, — мета-стабильной и мета-нестабильной, с проявлением в рамках последней самоорганизации первичных микроочагов разрушения, накопленных на меж-блоковом контакте. Наличие кооперативных явлений на таком микроуровне перед импульсной активизацией межблокового контакта подтверждается и последними результатами математического моделирования (Zang et al., 2026).

На основе результатов физического моделирования процессов формирования зон разломов в упруговязкопластичных моделях литосферы, а также результатов мониторинга деформаций горных пород и сейсмичности на геодинамических полигонах и с учетом выше отмеченных результатов китайских ученых, авторами предложена тектонофизическая модель очага тектонического землетрясения с вытекающим из неё краткосрочным предвестником (Борняков и др., 2024). В качестве такого предвестника выступает низкочастный автоволновой процесс, порождаемый деформационной самоорганизацией активизированных сегментов в очаге землетрясения в его критическом предсейсмогенном состоянии. С целью подтверждения наличия такого автоволнового эффекта авторами выполнено физическое моделирование процесса сейсмогенной активизации разлома по механизму “stick-slip” в упруговязкопластичной модели.

Методика физического моделирования и методы обработки

На рисунке 1 представлены схема экспериментальной установки (А) и её фото (Б). Установка состоит из двух штампов 1 и 2 с вертикальными торцевыми стенками для закладки модельного материала, перемещающихся без трения по подстилающим их роликам по направлению действующей нагрузки. Размеры штампов составляют (длина, ширина и высота) составляют 1.1 м х 0.2 м х 0.07 м и 0.8 м х 0.2 м х 0.07 м соответственно.

Заложение модельного разлома до начала эксперимента осуществлялось путем установки между активным и пассивным штампами перегородки из тонкого листового металла и ее выемки после размещения на штампах модельного материала. Для улучшения межблокового контакта после удаления перегородки проводилось поджатие пассивного блока на величину u₂, равную 10 мм (рис. 1 Б). На рисунке 2 показан общий вид экспериментальной установки до начала эксперимента. Активный штамп через пружину заданной жесткости k₁ соединялся металлическим тросом с электроприводом, обеспечивающими заданную скорость перемещения троса u₁(t). Для измерения усилия использовался тензодатчик (модель CZL 302), с диапазоном измерения 0–30 кг с погрешностью 0.01 кг, размещенный между штампом и пружиной k₁. Второй штамп (пассивный) также через пружину заданной жесткости k₂, крепился к неподвижной опоре. Таким образом, заданная конфигурация креплений штампов обеспечивала возможность поступательного смещения обоих штампов по подстилающим их фторопластовым роликам модельного разлома до некоторой критической величины, определяемой жесткостью второй пружины и свойствами модельного материала, после чего происходила динамическое смещением крыльев модельного разлома.

В качестве модельного материала была использована водная паста монтмориллонитовой глины, правомерность использования которой для тектонического моделирования обоснована в (Семинский, 1986).

Выбор граничных условий эксперимента осуществлялся в соответствии с критерием подобия (Гзовский, 1975; Шерман, 1984):

,                            (1)

где  – вязкость среды,  – плотность среды,  – ускорение свободного падения,  – линейные размеры,  – время,  – коэффициент подобия вязкости,  – коэффициент подобия плотности,  – коэффициент подобия ускорения свободного падения,  – коэффициент подобия линейных размеров,  – коэффициент подобия времени. Коэффициенты подобия представляют собой отношения параметров модели и натурного объекта. В данном исследовании коэффициенты подобия составляли: для вязкости – , для плотности – , для ускорения свободного падения , для линейных размеров –  и для времени . При таких значениях коэффициентов подобия 1 миллиметр в модели соответствует 100 метрам в ее природном аналоге, а 1 секунда эксперимента эквивалента 16–17 годам природного процесса. Заметим, что эти условия подобия пригодны для тектонической составляющей моделируемого процесса, но не применимы для интерпретации его динамической составляющей.

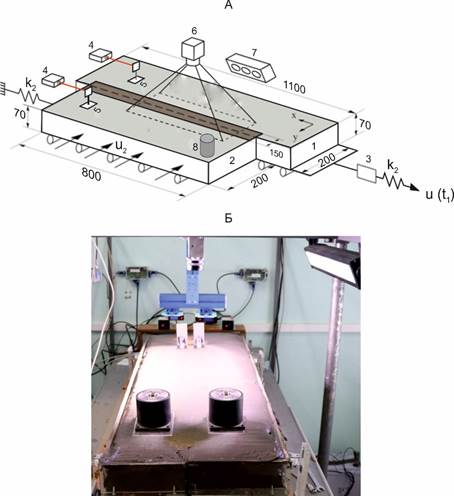
Рис. 1. Схема экспериментальной установки для моделирования процесса периодической импульсной активизации межблокового контакта в упруговязкопластической модели (А) и фото модели до начала эксперимента (Б). 1 – активный блок, 2 – пассивный блок, 3 – динамометр, 4 – лазерные дальномеры, 5 – отражатели, 6 – цифровая камера, 7 – светодиодная лампа, 8 – акселерометр, К₂ – пружины.

Fig. 1. Schematic diagram of the experimental setup for simulating the process of periodic pulsed activation of interblock contact in the elastic-viscoplastic model (A) and a photo of the model before the experiment (Б). 1 – active block, 2 – passive block, 3 – dynamometer, 4 – laser rangefinders, 5 – reflectors, 6 – digital camera, 7 – LED lamp, 8 – accelerometer, K₂ – springs.

Для мониторинга процесса подготовки и реализации подвижки по модельному разлому были использованы три метода инструментальной регистрации. Для оценки интегрального смещения каждого штампа использованы лазерные дальномеры Dimetics DPE-10 (рис. 1 А, 4). Фотофиксация свободной поверхности модели в процессе ее деформирования осуществлялась цифровой камерой Basler acA2440-75uс с объективом SV-2514H, имеющая максимальную частоту съемки 70 Гц и разрешение 5 Мпикс (рис. 1 А, 6). Съемка выполнялась со скоростью 30 кадров в секунду. Для получения высококонтрастного изображения свободной поверхности модельной среды на ее свободную поверхность насыпался тонкий слой речного песка мелкой фракции, который непрерывно освещался светодиодной лампой (рис. 1 А, 7).

Анализ локальных полей перемещений на свободной поверхности модельной среды в процессе ее деформирования проводился методом корреляции цифровых изображений (Digital Image Correlation - DIC) (Chao, Sutton, 1988; Choi, Shah, 1997; Lyons et al., 1996). Этот метод позволяет с высокой точностью восстанавливать эволюцию перемещений и деформаций на поверхности образцов из различных материалов при различных видах нагружения. Математический аппарат метода DIC изложен, например, в (Sutton et al., 2009).

Предварительная обработка и последующий анализ оптических изображений осуществлялись в специализированном программном обеспечении StrainMaster LaVision. На рисунке 2 показано распределение интегральной деформации сдвига в модели, рассчитанной по двум разнесенным по времени фотографиям.

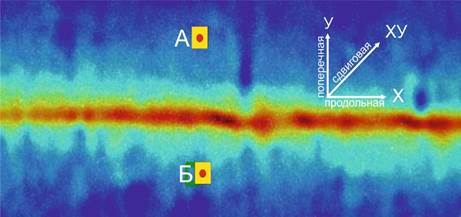
Рис. 2. Распределение интегральной деформации сдвига (ХУ) в модели при активизации модельного разлома. Красные точки в белых квадратах- реперные точки в активном (точка А) и пассивном (точка Б) крыльях модельного разлома, для которых рассчитывались продольная (Х) и поперечная (У) деформации. Для регистрации микросейсмических колебаний модели при реализации импульсного смещения по модельному разлому использовалась сейсмостанция «Байкал-8L» с пьезоэлектрическим акселерометром А1638. Данный комплект позволяют регистрировать ускорение смещения исследуемого объекта в полосе частот 0.1-400 Гц и в диапазоне амплитуд от 2*10^-5 м/с² до 2 м/с².

Fig. 2. Distribution of the integral shear strain (XY) in the model during activation of the model fault. Red dots in white squares are reference points in the active (point A) and passive (point Б) wings of the model fault, for which the longitudinal (X) and transverse (Y) strains were calculated. To record microseismic vibrations of the model during the implementation of pulsed displacement along the model fault, a Baikal-8L seismic station with an A1638 piezoelectric accelerometer was used. This kit allows recording the acceleration of displacement of the studied object in the frequency band of 0.1-400 Hz and in the amplitude range from 2* 10^-5 m/s² to 2 m/s².

Результаты

Результаты обработки серий фотографий методом корреляции цифровых изображений, показали, что деформационный процесс в модели реализуется в колебательном режиме, несмотря на нагружение активного штампа экспериментальной установки с постоянной скоростью. Для примера на рисунке 3 приведен график вариаций продольной деформации в активном и пассивном крыльях, рассчитанной для точек А и Б соответственно (рис. 2).

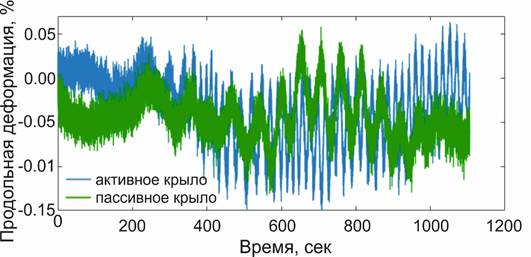
Рис. 3. Пример реализации продольной деформации в активном и пассивном крыльях модельного разлома в ходе эксперимента.

Fig. 3. An example of the implementation of longitudinal deformation in the active and passive wings of a model fault during an experiment.

Из графика следует, что частоты колебаний в активном и пассивном крыльях после 250 секунды эксперимента начинают существенно отличаться. Частота колебаний в первом из них (0.01 Гц) была меньше в два раза, чем во втором (0.02 Гц) между 250 и 350 секундами, а в дальнейшем это их соотношение увеличилось до трех (0.02 Гц и 0.06 Гц соответственно), на фоне примерно равного роста амплитуды колебаний в обоих крыльях. Увеличение амплитуды колебаний, обусловленное ростом напряжений в модели, фиксировалось до 850 секунд эксперимента, после чего она начала уменьшаться. Последнее связано со снижение их уровня за счет начала активизации модельного разлома. Его активизация начинается в дистальных окончаниях в краевых частях модели и постепенно распространяется в его центральные части. Во временных рядах данных с лазеров и с датчика грузки отсутствуют резкие изменения фиксируемых ими параметров, что указывает на равномерный, крипповый характер смещений по активизирующемуся модельному разлому. В тоже время, данные с сейсмодатчика, показывают наличие эпизодических импульсных смещений на его плоскости. Эти локальные очаги разрушения и разгрузки напряжений находятся в глубине модели и не выходят на её поверхность. Каждому импульсному смещению как акту разгрузки накопленных напряжений предшествует временной интервал «энергетической накачки», в пределах которой имеет место автоколебательный процесс, проявляющийся в виде биений с периодом 30–55 секунд с его понижением до 6–11 сек перед разгрузкой (рис. 4 А). Максимальные амплитуды автоколебательного процесса в период предваряющий разгрузку составляют для компоненты Х: Ах=2.461*10^-3 мм, для У: Ау=2.828*10^-3 мм, для Z: Аz=1.596*10^-3 мм, векторная амплитуда Axyz=0.004 мм. Характеризующий его спектр колебаний, без учета «разгрузки» показан на рисунке 4 Б. Видно, что он имеет структуру с двумя максимумами, равными 3.9 Гц и 7.8 Гц (рис.4 Б).

На рисунке 5 приведён пример непосредственно импульсного смещения по модельному разлому (А) и его спектр (Б). Основная часть колебаний находится в полосах частот 6.8–9.8 Гц и 12.7–14.6 Гц. При этом амплитуды колебаний равны для компоненты Х: Ах=3.138*10^-3 мм, для У: Ау=9.46*10^-3 мм, для Z: Аz=2.686*10^-3 мм, векторная амплитуда Axyz=0.01 мм. Из первого графика видно, что непосредственно перед смещением происходит увеличение амплитуды колебаний в 1.5 раза, что подчеркивается красными штрих-пунктирными кривыми (рис. 5 А).

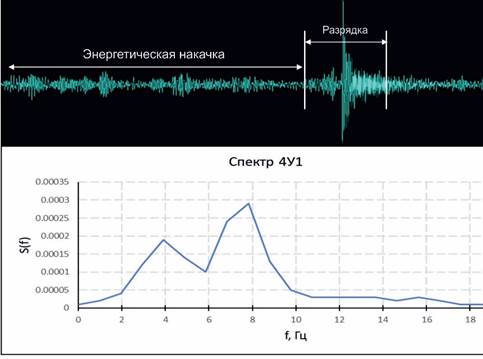
Рис. 4. Характерный пример процесса «энергетической накачки» с последующей разрядкой.

Fig. 4. A typical example of the process of “energy pumping” followed by discharge.

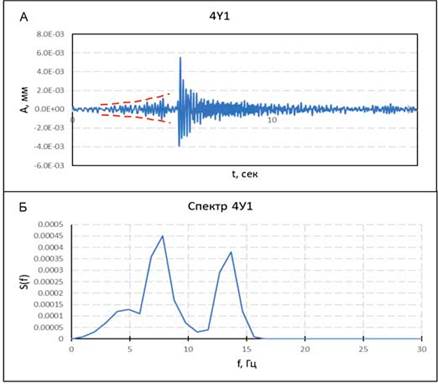
Рис. 5. Процесс энергетической разрядки (А) и его спектр (Б).

Fig. 5. The process of energy discharge (A) and its spectrum (Б).

Выводы

Выполненное физическое моделирование сейсмогенной активизации разлома по механизму “stick-slip” в упруго-пластичной модели литосферы с комплексной инструментальной регистрацией деформационного процесса в модели позволило установить что:

— деформации в крыльях модельного разлома реализуются в низкочастотном колебательном режиме, при постоянной скорости нагружения модели, с отличающимися частотами и амплитудами колебаний в активном и пассивном крыльях;

— рост напряжений в модели сопровождается уменьшением частоты колебаний и увеличением их амплитуды;

— импульсная активизация модельного разлома предваряется автоволновым деформационным процессом в высокочастотной области (4–14 Гц) с последующим уменьшением преобладающих частот в 2 раза и ростом амплитуды в 1.5 раза.

Литература

Гзовский М.В. Основы тектонофизики. М.: Наука, 1975. 536 с.

Семинский К.Ж. Структурно-механические свойства глинистых паст как модельного материала в тектонических экспериментах. Иркутск: ИЗК СО АН СССР, 1986. 130 с.

Соболев Г.А., Пономарев А.В. Физика землетрясений и предвестники. М. : Наука, 2003. 270 с.

Шерман С.И. Физический эксперимент в тектонике и теория подобия // Геология и геофизика. 1984. № 3. С. 8–18.

Bak P., Tang C., Earthquakes as a self-organized critical phenomenon // Journ. Geoph. Res. 1989. 94 (B11), 15635–15637. https://doi.org/10.1029/JB094iB11p15635

Brace W.F., Byerlee J.D. Stick-slip as a mechanism for earthquake // Science. 1966. V. 153. P. 990–992.

Chao Y.J., Sutton M.A., 1988. Measurement of strains in a paper tensile specimen using computer vision and digital image correlation—part 1: data acquisition and image analysis system. Tappi J. 70 (3). 173–175

Choi S., Shah S.P., 1997. Measurement of deformations on concrete subjected to compression using image correlation. ExpMech. 37 (3). 307–313.

Cicerone R.D., Ebel J.E., Britton J. A systematic compilation of earthquake precursors // Tectonophysics. 2009. Vol. 476. P. 371–396.

Geller R.J., Jackson D.D., Kagan Y.Y, Mulargia F. 1997. Earthquakes cannot be predicted. Science, 275(5306): 1616– 1616. https://doi.org/10.1126/science.275.5306.1616

Lyons J.S., Liu J., Sutton M.A., 1996. High-temperature deformation measurements using digital-image correlation. ExpMech. 36 (1). 64–70.

Ma J, Sherman S.I, Guo Y.S., 2012. Identification of meta-instable stress state based on experimental study of evolution of the temperature field during stick-slip instability on a 5^o bending fault. Sci China Earth Sci, 55: 869–881.

Sutton M.A., Orteu J.J., Schreier H.W., 2009. Image Correlation for Shape, Motion and Deformation Measurements: Basic Concepts, Theory and Applications. Springer. 316 p.

Zhang Y., Li Z., Gao K., Tang H., Li C., Wan Z. Solid-like to liquid-like transition of stick-slips in sheared fault gouge // Computers and Geotechnics. 2026. V.190. 107697.

 

Борняков Сергей Александрович,

кандидат геолого-минералогических наук,

664033, Иркутск, ул. Лермонтова, д. 128,

Институт земной коры СО РАН,

ведущий научный сотрудник,

тел.: (3952)42-63-81,

еmail: bornyak@crust.irk.ru

 

Пантелеев Иван Алексеевич,

доктор ф-м. наук,

664033, Пермь, ул. Ленина, 13а,

ПФИЦ УРО РАН,

Зав. лаб. цифровизации горнотехнических процессов,

тел.: +7(3422) 378317,

еmail: pia@icmm.ru

 

Шагун Артем Николаевич,

664033, Иркутск, ул. Лермонтова, д. 128,

Институт земной коры СО РАН,

ведущий инженер,

тел.: (3952)42-58-23,

 

Салко Денис Владимирович,

664033, Иркутск, ул. Лермонтова, д. 128,

Институт земной коры СО РАН,

ведущий инженер,

тел.: (3952)42-58-23,

еmail: denis@salko.net

 

Каримова Анастасия Алексеевна,

кандидат геолого-минералогических наук,

664033, Иркутск, ул. Лермонтова, д. 128,

Институт земной коры СО РАН,

младший научный сотрудник,

664003, Иркутск, ул. Карла Маркса, 1,

Иркутский государственный университет,

доцент,

тел.: (3952)42-63-81,

еmail: geowomen_nasty@mail.ru

Полный текст статьи (Русский)